How To Implement A Fir Filter In C

EECS20N: Signals and Systems

Implementation of FIR filters

Consider an FIR filter with impulse response h and input ten, where the output is given past

We now examine a number of means to implement this filter.

Matlab implementation

If x is finite, and nosotros can translate it as an infinite signal that is zero outside the specified range, then we can compute y using Matlab's conv() part. That is, if x is a vector containing the N values of the input, h is a vector containing the M + 1 values of the impulse response, then

y = conv(x, h);

yields a vector containing G + N values of the output. This strategy, of course, but works for finite input data.

Java implementation

The following Coffee class implements an FIR filter.

1	class FIR { ii	    private int length; 3	    private double[] delayLine; 4	    private double[] impulseResponse; 5	    private int count = 0;  half-dozen	    FIR(double[] coefs) { 7	        length = coefs.length; viii	        impulseResponse = coefs; 9	        delayLine = new double[length]; 10	    }  11	    double getOutputSample(double inputSample) { 12	        delayLine[count] = inputSample; xiii	        double upshot = 0.0; 14	        int index = count; 15	        for (int i=0; i<length; i++) { 16	            result += impulseResponse[i] * delayLine[index--]; 17	            if (alphabetize < 0) index = length-1; xviii	        } nineteen	        if (++count >= length) count = 0; 20	        render result; 21	    } 22	}

A form is Java (and in any object oriented linguistic communication) has both data members and methods. The methods are procedures that operate on the data members, and may or may non have arguments are return values. In this instance, at that place are two procedures, "FIR" and "getOutputSample". The start, lines 6-10, is a constructor, which is a procedure that is chosen to create an FIR filter. Information technology takes ane argument, an array of double-precision floating-betoken numbers that specify the impulse response of the filter. The second, lines 11-22, takes a new input sample value every bit an argument and returns a new output sample. It also updates the delay line using a strategy called circular buffering. That is, the count fellow member is used to keep runway of where each new input sample should become. It gets incremented (line 19) each time the getOutputSample() method is called. When it exceeds the length of the buffer, information technology gets reset to zero. Thus, at all times, it contains the M + 1 well-nigh recently received input data samples. The most contempo one is at index count in the buffer. The second most recent is at count − 1, or if that is negative, at length − ane. Line 17 makes sure that the variable index remains within the confines of the buffer as we iterate through the loop.

Programmable DSP implementation

The post-obit department of code is the assembly language for a programmable DSP, which is a specialized microprocessor designed to implement indicate processing functions efficiently in embedded systems (such as cellular telephones, digital cordless telephones, digital audio systems, etc.). This item code is for the Motorola DSP56000 family of processors.

one	fir	movep		10:input,x:(r0) 2		clr a		x:(r0)-,x0	y:(r4)+,y0 3		rep m0 4		mac x0,y0,a	x:(r0)-,x0	y:(r4)+,y0 v		macr x0,y0,a	(r0)+ vi		movep a,x:output 7		jmp fir

The code is explained beneath, line by line. While reading this, it will be helpful to know that this processor has two retentivity banks that can be separately addressed, called "ten" and "y". The lawmaking assumes that each input sample tin exist successively read from a memory location called "input", and that the impulse response is stored in y memory starting time at an accost stored in register "r4". Moreover, it assumes that register "r0" contains the address of a section of 10 retention to use for storing input samples, and that this annals has been set upwards to perform modulo addressing. Modulo addressing ways that if it increments or decrements beyond the range of its buffer, and so the address wraps around to the other terminate of the buffer. Finally, information technology assumes that the register "m0" contains an integer specifying the number of samples in the impulse response minus 1.

This line has a label, "fir", that is used in line 7 as a target for a jump. It begins the filtering performance by moving a new input data sample from a location in x memory to another location in x memory, where the accost of the destination is contained past the register named "r0".
This line clears (sets to cypher) a annals chosen "a", the "accumulator". At the same time, it loads a register named "x0" with a value from 10 memory, where the address in retentiveness is independent by register "r0". Then it decrements "r0". At the same time, register "y0" is loaded from a memory location given past "r4", and then "r4" is incremented to indicate to the side by side college location.
This line causes the post-obit line (line four) to be repeatedly executed a number of times, where the number of times is contained by the register named "m0".
This line does nearly of the work. Information technology multiplies the information contained in "x0" by that in "y0" and adds the outcome to "a" (such an operation is chosen a multiply and accumulate or mac operation). At the aforementioned time, it loads "x0" and "y0" with a new input sample and impulse response sample, much as done in line 2. As information technology executes repeatedly, it multiplies and accumulates new information.
This performs the last multiply and accumulate.
This writes the output data to a memory location called "output".
This restarts the filter so that it can process the side by side sample.

Digital hardware implementation

An FIR filter can exist hands implemented using just three digital hardware elements, a unit of measurement filibuster (a latch), a multiplier, and an adder. The unit delay only updates its output one time per sample menses, using the value of the input as its new output value. In the convolution sum,

notice that at each n we demand access to x(n), x(n − 1), x(n − 2), �, ten(due north − M). We can maintain this set up of values past cascading a set of latches to form a filibuster line, every bit shown below:

For each integer northward, the output sample is the values in the delay line scaled by h(0), h(i), �, h(1000). To obtain these values, nosotros only tap the delay line, as shown in the following film

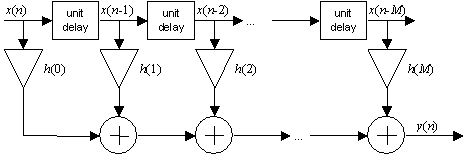
The triangular boxes denote multipliers that multiply by a constant (h(m)). The circles announce adders. The above picture shows a tapped delay line implementation of an FIR filter.